DÍZIMA PERIÓDICA

Queridos alunos dos 8º anos A, B e C da Escola Municipal Dom Manoel da Silva Gomes, sejam bem-vindos ao ano letivo de 2019!!! Vamos começar a disciplina de Matemática com o assunto Dízima Periódica e Fração Geratriz. Esse material da Professora Rosimar Gouveia é excelente ... dêem uma olhada!!

Dízima Periódica

Rosimar Gouveia

Professora de Matemática e Física

As dízimas periódicas são números decimais periódicos, ou seja, apresentam um ou mais algarismos que se repetem na mesma ordem infinitamente. O algarismo que se repete é chamado de período.

Os números decimais periódicos pertencem ao conjunto dos números racionais (), pois podem ser escritos na forma de fração. Por exemplo, o número 0,444... também pode ser escrito como .

Quando um número é decimal infinito, mas não apresenta algarismos que se repetem, ou seja, não possui um período, ele não será um dízima periódica e sim um número irracional.

Dízimas periódicas simples e compostas

A dízimas são chamadas de simples quando apresentam a parte inteira e após a vírgula apenas algarismos que se repetem.

São exemplos de dízimas periódicas simples:

• 0,34343434... → parte inteira igual a 0 e período igual a 34
• 1,222222... → parte inteira igual a 1 e período igual a 2
• 234,193193193... → parte inteira igual a 234 e período igual a 193

Já as dízimas periódicas compostas possuem a parte inteira e depois da vírgula algarismos que não se repetem, além dos algarismos que se repetem.

São exemplos de dízimas compostas:

• 3,125555... → parte inteira igual a 3, parte não periódica igual a 12 e período igual a 5.
• 1,7863333... → parte inteira igual a 1, parte não periódica igual a 786 e período igual a 3.
• 11,2350505050... → parte inteira igual a 11, parte não periódica igual a 23 e período igual a 50.

Representação das dízimas periódicas

As dízimas podem estar escritas na forma de fração geratriz ou na forma de número decimal. Quando estiver escrita na forma decimal, colocamos três pontinhos no final para indicar que os algarismos se repetem infinitamente.

Podemos ainda representar esse tipo de número colocando um traço horizontal apenas em cima do seu período.

Exemplos

Fração Geratriz

Rosimar Gouveia

Professora de Matemática e Física

Fração geratriz é aquela que quando dividimos seu numerador pelo denominador, o resultado será uma dízima periódica (número decimal periódico).

Os números decimais periódicos apresentam um ou mais algarismos que se repetem infinitamente. Esse algarismo ou algarismos que se repetem representam o período do número.

Quando o parte decimal é composta apenas pelo período, a dizima é classificada como simples. Já quando além do período existir, na parte decimal, algarismos que não se repetem, a dízima será composta.

Exemplos

Cálculo da fração geratriz

Encontrar a fração geratriz de uma dízima periódica muitas vezes é necessário para que possamos efetuar cálculos, por exemplo, em expressões numéricas.

Para descobrir a fração geratriz de uma dízima periódica simples, podemos seguir os seguintes passos:

• 1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau.
• 2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos "andar" para que o período fique antes da vírgula.
• 3º passo: Diminuir a equação encontrada da equação inicial.
• 4º passo: Isolar a incógnita.

Exemplos

1) Encontre a fração geratriz do número 0,8888...

Solução

Primeiro vamos escrever a equação do 1º grau, igualando o número a x:

x = 0,8888...

Observe que o período é composto por um único algarismo (8). Assim sendo, temos que "andar" apenas uma casa para ter o período na frente da vírgula. Assim, multiplicaremos a equação por 10.

10 x = 10 . 0,8888...
10 x = 8,888...

Agora vamos diminuir as duas equações, ou seja:

Isolando o x, encontramos a fração geratriz:

2) Transforme o número decimal 0,454545... em fração.

Solução

Iremos seguir os mesmos passos do exemplo anterior. A única diferença é que agora o período é composto de 2 algarismos (45). Neste caso, teremos que "andar" duas casas, e então iremos multiplicar por 100.

x = 0,454545...
100 x = 100 . 0,454545...
100 x = 45,454545...

Subtraindo as equações:

Isolando o x, descobrimos que a fração geratriz é igual a . Podemos ainda simplificar esta fração dividindo o numerador e o denominador por 9.

Assim, temos:

Quando a dízima periódica for composta, além dos passos indicados para a simples, devemos também multiplicar a primeira equação por um número múltiplo de 10, que a transforme em uma dízima simples.

Acompanhe o exemplo abaixo:

Qual a fração geratriz de 2,3616161...?

Solução

Neste exemplo, a dízima periódica é composta, pois o algarismo 3, que aparece depois da vírgula, não se repete.

Escrevendo a equação inicial, temos:

x = 2,3616161...

Como a dízima é composta, devemos primeiro multiplicar essa equação por 10, pois com isso, passamos o 3 para a frente da vírgula (algarismo que não se repete).

10 x = 23,616161...

Agora vamos escrever a outra equação multiplicando ambos os lados da equação inicial por 1000, pois assim, conseguimos passar o período para a frente da vírgula.

1000 x = 2361,616161...

Em seguida, faremos a subtração dessas duas equações e isolaremos o x para encontrar a fração geratriz.

Método Prático

Para encontrar a fração geratriz de uma dízima periódica, podemos também utilizar um método prático.

Quando a dízima for simples, o numerador será igual a parte inteira com o período menos a parte inteira, e no denominador, a quantidades de "noves" igual ao número de algarismo do período.

Exemplos

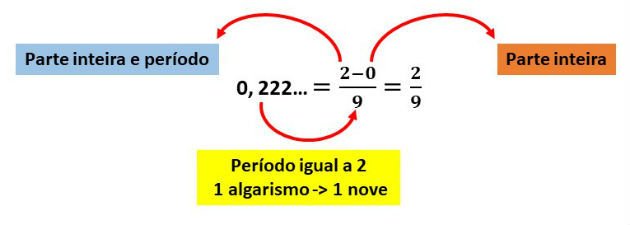
1) Determine a fração geratriz da dízima periódica 0,222...

Solução

Para encontrar a fração geratriz, vamos usar o método prático conforme esquematizado abaixo:

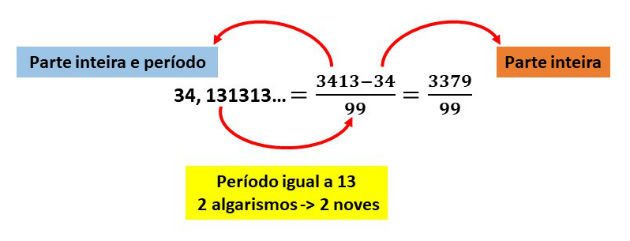
2) Qual a fração geratriz da dízima periódica 34,131313...?

Solução

Acompanhe o esquema abaixo para encontrar a fração geratriz.

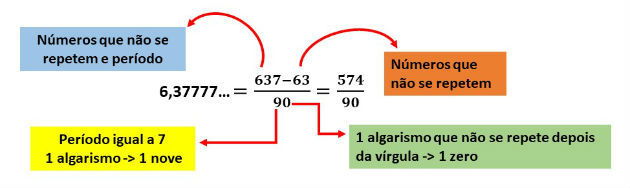
Quando a dízima for composta, o numerador será igual a parte que não se repete com o período, menos a parte que não se repete.

Exemplo

Encontre a fração geratriz da dízima periódica 6,3777...

Solução

Como a dízima periódica é composta, encontraremos a fração geratriz utilizando o seguinte esquema:

Agora ... vamos praticar: 

 Exercícios

 1 - Um estudante se cadastrou numa rede social na internet que exibe o índice de popularidade do usuário. Esse índice é a razão entre o número de admiradores do usuário e o número de pessoas que visitam seu perfil na rede. Ao acessar seu perfil hoje, o estudante descobriu que seu índice de popularidade é 0,3121212... Escreva esse índice na forma de uma fração geratriz

2 – Determine a fração geratriz que é o resultado da soma:   1,3333... + 0,16666...  

3 - Encontre a fração geratriz das dízimas indicadas abaixo:

a) 4,5555...
b) 7,38282...

c) 0,8222...

d) 1,212121...